LoadBalancing¶

Parallele Anwendungen im Bereich hoher Skalierung haben typischerweise mit mehreren Performanceproblemen zu tun: Die relative Bedeutung serieller An­teile steigt, globale Kommunikation skaliert nicht mit, und die Partitionsgrößen der einzelnen Tasks werden zunehmend kürzer und unterschreiten die Ausdeh­nung lokaler Lastschwankungen, die sich bei den größeren Partitionen einer niedrigeren Skalierung oft ausgeglichen haben.

Das Problem der Lastschwankungen ist verwandt mit dem Nachteil eines seriel­len Anteils, da in beiden Fällen der Prozess mit der maximalen Last die Ge­samtausführungszeit bestimmt. Viele Simulationsmodelle sind jedoch in einer Zeit enstanden als dieses Problem von untergeordneter Bedeutung war. Auf­grund der hohen Komplexität dieser Modelle gestaltet sich eine radikale Anpas­sung an aktuelle Anforderungen jedoch schwierig, daher muss man bei der Aus­wahl der Verfahren zum Lastausgleich auch die Realisierbarkeit für vorhandene Modelle berücksichtigen. Im Falle der hier betrachteten Kli­mamodelle bedeutet dies, möglichst viele Aspekte einer regulären Zerlegung beizubehalten.

reguläre Dekomposition des TP04L40 Gitterraumes mit 16x8 Prozessoren

Lastangepasste Dekomposition des TP04L40 Gitterraumes mit 16x8 Prozessoren

In der Nord-Süd Richtung bleiben die einfachen Nachbarschaftsverhältnisse erhalten. Die Ost-West Nachbarschaft beschränkt sich auf feste Prozessgruppen. Jeder Prozess bearbeitet ein rechteckiges Gebiet. Breite und Höhe aller Teilgebiete können eingeschränkt variieren.

Lastverteilung im Prozessraum betrachtet:

Relative Abweichung der Prozessorlast von der mittleren Last für die reguläre Dekomposition

Relative Abweichung der Prozessorlast von der mittleren Last für die lastangepasste Dekomposition

Das eingesetzte einfache Verfahren ist in der Lage die Last­schwankungen im 16x8 Prozessorgrid nahezu vollständig auszugleichen
Die Effektivität des Lastausgleichs wird durch die Variierbarkeit der Teilge­biete begrenzt. Bei sehr hoher Skalierung wird eine Verschiebung einer Gebietsgrenze um einen Gitterpunkt zu einer relativ groben Variation, dann wird ein Lastaus­gleich schwierig:

Theoretischer Speedup aus der Lastanalyse

Dynamischer Lastausgleich:

In dem betrachteten Atmosphärenmodell ECHAM treten statische und dynamische Lastanteile auf. Hier ist z.B. die Behandlung der Landoberfläche deutlich auf­wendiger (statische Last). Zu den dynamischen Effekten gehört z.B. die sehr aufwendige kurzwellige Strahlung, die nur jeden 12. Zeitschritt berechnet wird und die Lastverteilung in diesem Zeitschritt völlig verändert (diese Strahlung ist prinzipiell auch abhängig von der Tag-/Nachtseite – dieser Unterschied wird aber zZ. im Modell nicht ausgenutzt).

Zu den physikalisch Ursachen für (quasi-) kontinuierliche Laständerungen gehören z.B.: Konvektion, barokline Instabilität (Wettersysteme der mittleren Breiten) – dies kann man z.B. über dem Meer sehen, innertropische Konvergenzzone.

Periodische Lastveränderungen (auch unstetige wie die Strahlungsberechnung) lassen sich durch vorausberechnete Dekompositionen ausgleichen. Kontinuier­liche Veränderungen (Physik) mit differenzierbaren Kostenfunktionen können je nach Zeitskala des physikalischen Prozesses extrapoliert werden (Vorher­sage).

Film zur dynamischen Lastverteilung: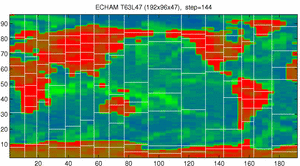

Der Film zeigt die relative Abweichung der Last vom Mittelwert im Gitter­punktsraum des Klimamodells ECHAM bei einer T63L47 Auflösung (192x96x47). Rot bedeutet Überlast, blau bedeutet Unterlast, und Grün mittlere Last. Im Idealfall (homogene Last) ist alles grün. Die eingezeichneten Parti­tionsgrenzen eines 16x8 Prozessorgrids sind nach der Simulation für jeden Zeit­schritt berechnet worden (also keine Extrapolation), um die tatsächliche Last­verteilung zu verdeutlichen. Man erkennt den Einfluss der Strahlungsberech­nung (Zeitschritt 1, 13, 25,37, …) und die kontinuierliche Lastverschiebung in jedem Zeitschritt.

Zur Extrapolation ist es nun notwending kurzzeitige Schwankungen herauszu­filtern, da die Dekomposition aus Effizienzgründen (MPI-Kommunikation) nicht nach jeden Zeitschritt angepasst werden kann.