Auswahl von Gebietszerlegungen¶

Bei der Wahl einer Dekompositionsmethode für das ScalES Projekt ist die leichte Integrierbarkeit in die vorhandenen hochkomplexen Klimasimulationsmodelle von besonderer Bedeutung. Wichtige Modelle sind das Ozean-Modell MPIOM [MPIOM-Report] mit zweidimensionalem Halo-Austausch und das spektrale Atmosphären-Modell ECHAM [MPI-Report 349] mit globalen dreidimensionalen Transpositionen.

Reguläre Zerlegung¶

Bisher wurde in diesen Modellen eine statische reguläre zweidimensionale Zerlegung eingesetzt. Diese ist für kleine Prozeßzahlen oder hinreichend homogene Last ( w(x(i),y(i)) = const ) oder hochfrequente Lastschwankungen mit relativ geringer Amplitude ausreichend.

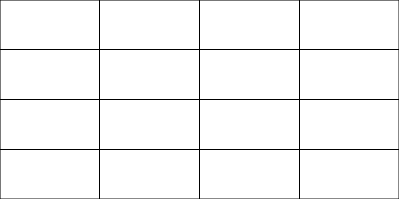
Quasi-Reguläre Zerlegung¶

Zur besseren Lastverteilung wurde zunächst eine allgemeinere, quasi-reguläre Zerlegung unter Beibehaltung der Partitionsnachbarschaft untersucht. Diese Zerlegung ist besonders geeignet, wenn die Anpassung der Modelle möglichst gering sein soll, da die Kommunikationsmatrix sowie die Rechteckgestalt der Teilgebiete erhalten bleiben. Es ändern sich lediglich die Datenvolumina. Die tatsächliche Last wird in diesem Verfahren als w(x(i),y(j)) == a(x(i)) x b(y(j)) approximiert.

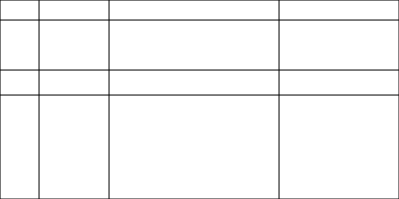
Mehrstufige Eindimensionale Zerlegung¶

In der Abfolge der Zerlegungen mit zunehmender Komplexität auf der Modellseite wurde eine mehrstufige eindimensionale Zerlegung untersucht. Diese kann man auch als hierarchische Zerlegung auffassen, da in jedem Zerlegungsschritt ein Gebiet entlang einer Unterdimension rekursiv weiter zerlegt wird, so dass sich das Zerlegungsproblem in jedem Schritt um eine Dimension reduziert. Die Nachbarschaft bleibt nur eingeschränkt erhalten. In der folgenden Abb. bleibt die Nachbarschaft in einer Dimension erhalten und beschränkt sich in der anderen Dimension auf feste Prozeßgruppen.

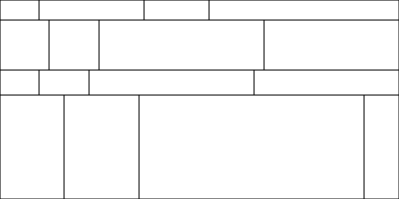
Im Gegensatz zu den vorherigen Verfahren erreicht man hiermit im Kontinuumslimes (unendlich hohe Gitterpunksauflösung bei begrenzter Lastschwankung) einen vollständigen Lastausgleich. Die Lösung läßt sich in diesem Fall analytisch einfach berechnen. Bei realistischer Auflösung ist es das Verhältnis von Gitterpunktsabstand und Breite der Lastpeaks, welches den Lastausgleich begrenzt. Hier wird zusätzlich ein iterativer Ansatz verfolgt, um die Kontinuumsapproximation zu optimieren.

Ein zusätzlicher Vorteil dieser speziellen Zerlegung ist die gute Abbildbarkeit auf die Kommunikationshierarchie aktueller Rechencluster. Z.B. kann die zuletzt zerlegte Dimension eines Teilgebietes vollständig einem Shared-Memory Knoten zugeordnet werden. Damit wird globale Kommunikation in dieser Dimension beschleunigt, so dass Modelle mit asymmetrischer Kommunikationslast (z.B. ECHAM) besonders unterstützt werden können.

Globale Summen, die das serielle Ergebnis exakt reproduzieren müssen, können in diesem Verfahren günstig über partitionsunabhängige Teilsummen berechnet werden.
Dieses Verfahren läßt sich außerdem gut parallelisieren und damit auch für eine dynamische Repartitionierung einsetzen.

[Halver] verwendet diese Art von Zerlegung in einem rein iterativen adaptiven Lastbalance-Verfahren für Molekulardynamik Simulationen im quasi-statischen Fall und mit kontinuierlich verschiebbaren Grenzen sowie stetiger Lastdichte. Die Annahmen lassen sich nicht auf die diskrete Last von Gittermodellen übertragen. Insgesamt erscheint sein Vorgehen für gitterbasierte Erdsystemmodelle wenig geeignet.

Mehrdimensionale Hierarchische Zerlegungen¶

Diese Zerlegungen sind flexibler bzgl. der Abfolge der Zerlegungsdimensionen und der Anzahl der Unterteilungen in jedem Teilgebiet und können daher mit der diskreten Last besser umgehen. Sie werden hier aber wegen des hohen Anpassungsaufwands der Modelle zunächst nicht weiter behandelt.

Graphpartitionierung¶

Die Graphpartitionierung betrachtet sowohl Rechenlast als auch lokale Kommunikationslast. Es wurde die Metis Bibliothek [METIS] verwendet, um eine statische Modell-Last (Tiefenschichten im Ozean) zu verteilen. Die enstehenden Partitionen sind zwar gute Lösungen des angenommenen Lastproblems, allerdings sind die Gebiete nicht rechteckig sondern beliebig geformt, so dass auf der Modellseite ein sehr hoher Aufwand zu erwarten ist. Diese Klasse von Verfahren wird daher zunächst zurückgestellt.

Literatur¶

MPIOM-Report:
http://www.mpimet.mpg.de/fileadmin/models/MPIOM/DRAFT_MPIOM_TECHNICAL_REPORT.pdf)¶

MPI-Report 349:
Roeckner, E., G. Baeuml, L. Bonaventura, R. Brokopf, M. Esch, M. Giorgetta, S. Hagemann, I. Kirchner, L. Kornblueh, E. Manzini, A. Rhodin, U. Schlese, U. Schulzweida, A. Tompkins,
The atmospheric general circulation model ECHAM5 - Part 1, MPI-Report 349, 127 pp, 2003.¶

Halver, Rene,
Adaptives Lastbalance-Verfahren für Gebietszerlegung in der Molekulardynamik,
Jül-4323, Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag, 2010
http://hdl.handle.net/2128/3732¶

METIS
http://glaros.dtc.umn.edu/gkhome/views/metis¶